by Christian Fenn, Hammelburg


In April 2005, I was busy with taking photographs of fogbows. Most of them I produced by the diverging light of my car headlights in the thick fog of the nearby meadows at the banks of the river Saale. As rainbows and fogbows form under very similar conditions, I thought that it also should be possible to observe rainbows in diverging light. I had never seen any pictures of this phenomenon, and so I got the ambition to shoot such a photograph.
When you are just sitting in your car looking ahead, absolutely nothing happens. But the one who does not spare the pains to walk a few metres in front of his car under the pouring rain will see that a rainbow forms around him from structures that are diffuse at first and become clearer and clearer the further he walks.
The rainbow was much too big for the photographical equipment I owned at that time, so that I could record my first observation of this bow only in form of a composed picture. In difference to parallel light, I could see this rainbow, which I first called “night rainbow”, really as a full circle for the first time, just as the theory always tried to teach us. If you look at the picture closely, you also can see the 51°-bow.
From haloes that appear in diverging light, I knew that light phenomena caused by artificial
Light sources have certain extensions that are to be put into a proportion between observer and lamp. So I was interested in the way this “night rainbow”, which I now call “lamplight rainbow”, is organized in space and where the rainbows responsible for its formation are localized.
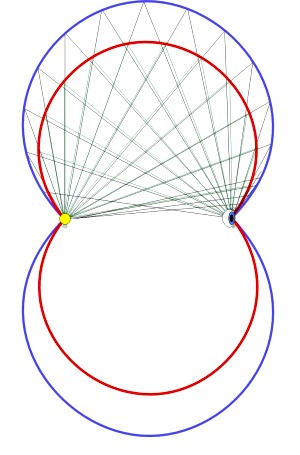
As I did not have the mathematical knowledge to evaluate such bows, I began to construct them at home. I drew rays extending from the light source into all possible directions. Then I looked for the point (raindrop) on the ray from where a refraction of 42° respectively 51° (138° resp. 129°) would fall directly into the eye of an observer. I got a figure resembling an apple, which according to Alexander Haußmann is called a “Minnaert-cigar”.
In the diagram, the blue curvature describes the inner 42°-rainbow and the red one the outer 51°-rainbow.
This, however, also meant that the rainbow would appear at many different places in space, from the observer's sight in all possible angles bigger than 42°, thus also at 43°, 44°, etc. The result should have been that all these rainbows should superimpose and thus disperse each other, as their colours should add up to white and the bows should not contrast from the background any more.
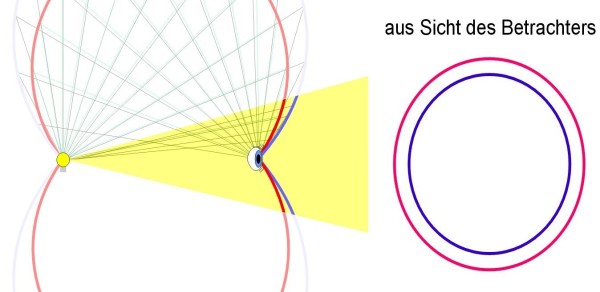
There are probably two reasons why they can be observed despite this. First, the water drops nearer to the eye (at an angle of 42° and a few degrees further to the outside) seem to add up more than for example those which are 90° away. Secondly, the car headlights do not illuminate the “apple” homogenuously, but in a relatively narrow cone. Thus the area right before the eye, which is already better added up, is also better illuminated (see diagram).
As a result, the “lamplight rainbow” can be clearly recognized, as proved by the photographs above.
As the car headlights are not of a punctuate shape, the bow appears slightly blurred. Additionally, as a car has two headlights, there are also two “Minnaert-cigars” lying side by side. As they add up, the bow perceptible is wider at the sides (see fig. 1).